Vector 활용

Normalize ( 정규화? 규격화? )

 (1, 2, 3) 이라는 3차원 백터를 노말라이즈 하는 과정

 1. 백터의 힘을 구한다

  vectorForce = sqrt(1*1 + 2*2 + 3*3)

  vectorForce = 3.74…. 정도가 나온다. 이것이 백터가 가진 힘(길이)!

 2. 이제 이 힘으로 각 원소를 나누어준다

  x = 1 / vectorForce

  y = 2 / vectorForce 

  z = 3 / vectorForce 

해서 나오는 (x, y, z) 가 노말라이즈 된 백터이다

(0.267, 0.534, 0.801) 라는 백터가 나온다

이 백터의 힘을 구해본다면 그 힘(길이)이 1이 나올 것

방향은 유지하고 힘(길이)을 1로 맞추는 과정이 Normalize

Dot Product ( 내적 )

두 백터를 가지고 계산하여 나오는 실수 값

내적의 활용도는 무궁무진, 그 이유는?!

1. 내적의 계산 방법

v1 = (a, b, c)

v2 = (x, y, z)

내적의 표기는 ->  v1 · v2 ( 가운데 점이다. 그래서 dot product )

계산법 (  각 원소를 같은 위치의 원소들과 곱하고 그것들을 모두 더한다 )

 1) v1 · v2 = a*x + b*y + c*z

 2) v1 · v2 = v1Force *  v2Force * cos(theta) 

2) 번 식이 상당히 중요함. 왜냐하면  cos 과 theta 개념이 탑재 되어 있기 때문

위 식에 나온  theta 는 v1 과 v2 의 사이각을 의미한다.

그렇다 그 사이각의 변화에 따라 내적값이 변경 된다.

아 내적은 두 백터의 관계가 수치로 표현 되는 것이구나!!

그렇다면 이 관계? 로 부터 어떤 수치가 나오는걸까?

이를 알아보기 위해 우선 2번 식을 간소화 해보자

위에서 언급한 Normalize 를 이용하면 v1Force 와 v2Force 를

1로 만들 수 있다는 것에 착안한다.

v1 과 v2 의 내적을 구하기 전에 각각을 normalize 하고 2번 식을 구성해보자

그러면  v1 · v2 = 1 *  1 * cos(theta) 이런 식으로 나오게 되고

결국은  v1 · v2 = cos(theta) 이렇게 되는것이다.

실제로 내적은 대부분 노말라이즈된 백터를 가지고 수행하는 것이 원칙이다.

결국 내적의 값은 코사인 함수에 그 사이각을 라디안 으로 대입하면 나오는

값이다. 

이제 코사인 곡선을 그려보자

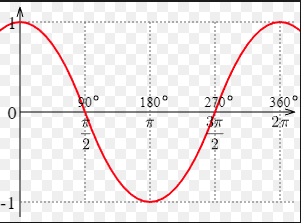
이 그래프를 잘 보면

cos() 의 괄호 안에 들어가는 라디안으로 표기 각도값에 따라

cos()  의 값이 1 과 -1 사이를 오르락 내리락 한다.

그렇다 내적은 -1 과 1 사이 값을 가진다.

사이각이 0, 즉 같은 방향의 백터들은 내적값이 1이고

사이각이 180도, 즉 반대 방향인 백터들의 내적은 -1

사이각이 직각을 이루는 경우는 0 이다.

내적 값은 알았고 반대로 theta 값 즉 두 백터의 사이각을 구하려면

어떻게 해야 할까

v1 · v2 = cos(theta) 을 바탕으로 양변에 acos를 곱해준다

acos( v1 · v2 ) = theta 가 된다

참고로 각도와 라디안 변화식은

180 가  π  라는 것을 기억한다면

1° = π / 180°

180° ->    180°  x  (π / 180) ->  π

0.5 rad -> 0.5 x (180 / π) -> 90 / π

Cross Product ( 외적 )

외적의 경우 계산후 실수값이 아닌 

두 백터에 모두 수직인 백터가 나온다 

1. 외적의 계산 방법

v1 = (a, b, c)

v2 = (x, y, z)

외적의 표기는 ->  v1 x v2 ( 가운데 x이다. 그래서 cross product )


활용법

1. 점과 직선의 최단거리








































2.점과 선분의 최단거리

3.